Think later | e2718281828459045

Maximum coverage of a fixed rectangle

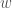Given a set $\mathcal{R}$ of non-overlapping rectangles on the plane, and two real numbers $w, h > 0$ , find a rectangle $R^{\ast}$ of of width $w$ and height 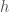$h$ , maximizing $\sum_{R \in \mathcal{R}} {\rm area}(R \cap R^{\ast})$ .

This is an interview question.

The first observation is that the upper side $R^{\ast}$ must coincide with the upper edge of some $R \in \mathcal{R}$ and the left side must coincide with the left edge of some rectangle in $\mathcal{R}$ . With this observation, we can already get an algorithm of time complexity $O(n^3)$ : enumerate over all possible choices of upper side and left side of $R^{\ast}$ , note that once the upper side and left side of $R^{\ast}$ is fixed, the rectangle $R^{\ast}$ is fixed (as we know its width and height). 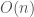There are $O(n)$ candidates for the upper side, and 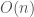$O(n)$ candidates for the left side, so there are $O(n^2)$ candidates of $R^{\ast}$ . 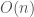For each candidate, we compute $\sum_{R \in \mathcal{R}} {\rm area}(R \cap R^{\ast})$ : this can be done in $O(n)$ time, as for each rectangle, we can determine in constant time the area of overlapping region of 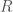$R$ and $R^{\ast}$ . So the overall time complexity is $O(n^3)$ .

But I feel that there should be faster algorithms. There are several reasons:
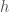(1) It feels quite inefficient to examine all rectangles for each of the $O(n^2)$ candidate rectangle. Maybe we could use the sweep-line algorithm: first sort the candidate of upper sides in time $O(n \log n)$ , then sweep a horizontal slab of height $h$ from north to south, where the state is the set of rectangles in 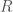$R$ overlapping the slap. For each slab, we again sweep the candidate rectangle from west to east, enumerating over all possible left sides of rectangles intersected by the current slab.
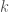(2) Using interval trees, one can query the rectangles intersected by a rectangle in time $O(\log n^2 + k)$ , where $k$ is the number of rectangles contained in the query rectangle.
(3) Perhaps we could also use other space partition data structures to quickly compute the overlapping area of a candidate rectangle.

My guess is that in the worst case, $O(n^2 \log n)$ time complexity algorithm should be possible, but I hope there would be a $O(n \log n)$ time complexity algorithm….

e2718281828459045

Category: Think later

September 19, 2013

Map tiling

September 11, 2013

Maximum coverage of a fixed rectangle