Notes 笔记 | e2718281828459045

An example of recursive definition

Recursive data types are ubiquitous in functional programming language. Two common examples are trees and lists. Here is a nice and slightly different example from “The Little MLer”:

datatype
   slist = 
   Empty
  |Scons of (( sexp) * ( slist))
and 
   sexp =
   An_atom of 
  |A_slist of ( slist)

Here $\alpha$ is a type variable. For example, we can let $\alpha$ be fruit, where fruit is a data type defined as

datatype fruit =
  Apple
 |Pear

The slightly strange thing about $\alpha$ slist is when you try to describe the set of values for this data type: if we say “ $\alpha$ slist is a set, which contains an element Empty, and Scons of pairs of $\alpha$ sexp and $\alpha$ slist…”–but this definition does not make much sense as we have not defined $\alpha$ sexp yet. If we try to define $\alpha$ sexp, we run into the same problem: “ $\alpha$ sexp is a set, which contains elements An_atom(x), where $x$ is of type $\alpha$ , and A_slists of $\alpha$ slist”–we have not defined what $\alpha$ slist yet.

The way to get out of this logical dilemma is to use induction. For example, for the type fruit slist and fruit sexp, we define the two sets as following:
(1) $A_0 = \{{\rm Empty}\}$ , $B_0 = \{{\rm An\_atom(Apple)}, {\rm An\_atom(Pear)}\}$
(2) $A_{i+1} = \{{\rm Scons}(x,y)\vert x \in \cup_{j=0}^i A_i, y \in \cup_{j=0}^i B_i\}$ ,
$B_{i+1} = \{{\rm A\_slist}(x) \vert x \in \cup_{j=0}^i A_i\}$ , $i \geq 1$ .

Then the set of values for fruit slist (resp. fruit sexp) is $\cup_{i=0}^{\infty}A_i$ (resp. $\cup_{i=0}^{\infty}B_i$ ).

A nice application of integer partition

Integer partition is a classic problem in enumeration. It often appears in an introduction to recursion/dynamic programming. For example, the coin exchange problem, where we are given a target sum $x$ , and a set of denominations, one can ask (1) is it possible to get the sum $x$ using the set of denominations; (2) how many ways are there to get the sum; (3) the smallest number of bills one need to get the sum; (4) enumerate all the ways to get the sum etc.

Here is another interesting application of integer partition (from “Understanding and using linear programming“): column generation. It is a preprocess step for linear programming problems. Consider the problem of cutting paper rolls. Suppose we have a list of 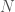$N$ orders of rolls with various width and number $\{(w_i, n_i) \vert 1 \leq i \leq N\}$ , where each order is specified by a pair $(w_i, n_i)$ , which means $n_i$ rolls of width $w_i$ (cm). We are going to cut these rolls from several large rolls of width $W$ . 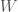Clearly, it can happen that some material might be wasted: for example, suppose the large roll has width 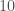$10$ . We can cut a roll of width 6 and a a roll of width 3, then the remaining roll of width 1 is wasted. One natural optimization problem here is to minimize the total number of large rolls we use to fulfill the orders. This problem can be solved by linear programming (approximately). Integer partition is used to form the linear programming problem.

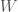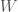To formulate the linear program, we enumerate all possible ways to cut the large roll of width $W$ into rolls of various widths from $\{w_i \vert 1 \leq i \leq n\}$ . For example, $w_1 + 2 w_3$ , $2 w_1 + w_2 + w_5$ , etc. each cut must obey the natural constraint, which means that their sum of widths cannot exceed the overall width $W$ , and at the same time they should be maximal in the sense that the remaining, for example, $W - (w_1+2w_3)$ is smaller than the minimum $\min_{1 \leq i \leq n} w_i$ . 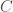For each a feasible cut plan $C$ of the large roll, we introduce a variable $x_C$ , which denotes that number of large rolls that will be cut according to this specification. So the optimization problem is $\min \sum_{C} x_C$ , where the summation is overall possible cut plans $C$ .

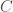The following example is from the book: suppose the large roll has width $W = 3$ m, the list of orders are:

97 rolls of width 135cm
610 rolls of width 108cm
395 rolls of width 93cm
211 rolls of width 42cm

The possible cut plans are:

P1: $2 \times 135$
P2: $135 + 108 + 42$
P3: $135 + 93 + 42$
P4: $135 + 3 \times 42$
$\cdots$
P12: $7 \times 42$

There are totally 12 possible cut plans, so the linear program will have 12 variables, each 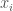$x_i$ denotes the number of large rolls that will be cut according to plan Pi. Naturally, the constraint would be formed according the number of each type of rolls required in the order.

The code to compute all possible cutting plans:

integerpartition :: [Int] -> Int -> [[Int]]
integerpartition _ 0 = [[]]
integerpartition [] _ = []
integerpartition [w] x = [replicate (x `div` w) w]
integerpartition weights@(maxelem:remain) x
    | maxelem > x = integerpartition remain x
    | otherwise = [maxelem:c | c <- integerpartition weights (x - maxelem)] ++ integerpartition remain x

Naturally, we should also have the constraint that each 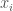$x_i$ should be integer. Once we get an optimal solution by solving the linear program, one possible solution is to round up each 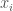$x_i$ to an integer.

e2718281828459045

Category: Notes 笔记

October 23, 2013

An example of recursive definition

September 27, 2013

A nice application of integer partition