The Task Scheduling problem is from Hackerrank.
Task Scheduling
Given a list of  tasks
tasks  , where the
, where the  task has deadline
task has deadline  and duration
and duration  , for each
, for each 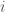 ,
,  , compute the minimum maximum lateness of the first
, compute the minimum maximum lateness of the first 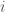 tasks.
tasks.
First we introduce some notations which will be used in the following discussion. Given a set  tasks, a schedule of the tasks is a sequence
tasks, a schedule of the tasks is a sequence  , where each
, where each  is in
is in ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=fff&fg=444444&s=0&c=20201002) . In other words, the sequence,
. In other words, the sequence,  is a permutation of
is a permutation of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=fff&fg=444444&s=0&c=20201002) . For example, a schedule for
. For example, a schedule for  , could be
, could be  (we first process task
(we first process task  , then
, then  , lastly,
, lastly, 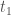 ). For a schedule
). For a schedule  , the start time for
, the start time for 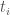 ,
,  , is
, is  (the summation of durations of all the tasks before task
(the summation of durations of all the tasks before task 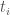 in the schedule), and the finish time
in the schedule), and the finish time  is
is  (the start time for
(the start time for 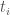 plus the time needed to process
plus the time needed to process 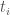 ). The lateness of
). The lateness of 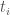 ,
,  for
for 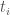 in this schedule is the difference between its finish time and its deadline,
in this schedule is the difference between its finish time and its deadline,  . Here is an example (the input is from Hackerrank). Suppose we have 5 tasks,
. Here is an example (the input is from Hackerrank). Suppose we have 5 tasks,  . The first task
. The first task 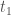 has a deadline at 2, and we need 2 time units to process
has a deadline at 2, and we need 2 time units to process 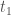 ; similarly, the second task
; similarly, the second task  has a deadline at 1, and its duration is 1, and so on. A valid schedule for these 5 tasks might be,
has a deadline at 1, and its duration is 1, and so on. A valid schedule for these 5 tasks might be,  . The start time
. The start time  , for
, for  is 0, and the finish time
is 0, and the finish time 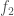 is 1, the lateness
is 1, the lateness  is
is  ; the start time
; the start time  for task
for task 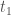 is 1 (which is the finish time of the task just precedes it), and the finish time
is 1 (which is the finish time of the task just precedes it), and the finish time 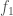 is
is  , so it has lateness
, so it has lateness  . Similarly, we can compute the start time/finish time/lateness for the rest of the tasks:
. Similarly, we can compute the start time/finish time/lateness for the rest of the tasks:  ,
,  ,
,  ;
;  ,
,  ,
,  ;
;  ,
,  ,
,  . So the maximum lateness,
. So the maximum lateness,  is 3, which is the lateness of
is 3, which is the lateness of  .
.
A Greedy Algorithm to Process a Set of Tasks
If we are given  tasks, and our goal is to find an optimum schedule for the
tasks, and our goal is to find an optimum schedule for the  tasks, we can solve this problem using the greedy algorithm: sort the tasks by deadlines in non-decreasing order, and that order is the schedule minimizing the lateness. The time complexity is
tasks, we can solve this problem using the greedy algorithm: sort the tasks by deadlines in non-decreasing order, and that order is the schedule minimizing the lateness. The time complexity is  .
.
The algorithm, which we will refer to  , is the following:
, is the following:

Input: a set of  tasks, each task
tasks, each task 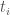 is specified by
is specified by 
Output: a schedule  , where
, where ![i_j \in [n]](https://s0.wp.com/latex.php?latex=i_j+%5Cin+%5Bn%5D&bg=fff&fg=444444&s=0&c=20201002) , and the maximum lateness
, and the maximum lateness  .
.
1. Sort the tasks by the deadlines, and renumbering these tasks. Let  be the new sequence of tasks.
be the new sequence of tasks.
2. 
3. 
4. for each 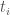 in
in 

if ( )
)

5. Output  and
and 
The time complexity of the above algorithm is  , as the first step, sorting, takes
, as the first step, sorting, takes  . The rest takes
. The rest takes 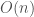 .
.
An Incremental Algorithm to Process  sets of tasks
sets of tasks
Let us now consider the Task Scheduling problem from Hackerrank. Here we need to compute the maximum lateness for  sets of tasks, that is, the first
sets of tasks, that is, the first 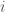 tasks, for each
tasks, for each  . For notational convenience, in the following, we use
. For notational convenience, in the following, we use  to denote the first
to denote the first 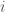 tasks. Note that
tasks. Note that  . The possible solutions might be:
. The possible solutions might be:
- The most naive method. Repeat
 for each
for each  , for
, for  . The time complexity is
. The time complexity is  , which is
, which is  .
.
- The relatively less naive method. Note that we don’t need to repeatedly do the sorting step: once we have the optimum schedule for
 , we can use binary search to find the position to insert
, we can use binary search to find the position to insert  , which takes
, which takes  . But we still have to update the lateness. How can we do this? Since all the tasks after the newly inserted task is delayed further by
. But we still have to update the lateness. How can we do this? Since all the tasks after the newly inserted task is delayed further by  time units, their lateness might increase. So if we scan all
time units, their lateness might increase. So if we scan all 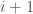 tasks to find the new maximum lateness, this would take
tasks to find the new maximum lateness, this would take  time. So the overall time complexity is
time. So the overall time complexity is  , which is
, which is  , which is
, which is  .
.
In the following, we describe an algorithm that takes  time and
time and 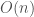 space. Note that the main difficulty is to update the lateness, which in turn involves two subproblems: (1) compute the lateness of the newly inserted task
space. Note that the main difficulty is to update the lateness, which in turn involves two subproblems: (1) compute the lateness of the newly inserted task  , so that we can compute its latesness
, so that we can compute its latesness  , and (2) compute the maximum lateness of all the tasks that are pushed
, and (2) compute the maximum lateness of all the tasks that are pushed  time units further to the right along the time line, because of the insertion of
time units further to the right along the time line, because of the insertion of  .
.
Let us first consider the first subproblem, which can be solved in logarithmic time in many ways. The easiest method to think of, is probably to use a balanced binary search tree (but note that we will use a better approach — a simpler one, although with the same time complexity). Given a list of tasks, we can build a vanilla balanced binary search tree  of the tasks, where the key is the deadline (this would allow us to find the correct position for the new task
of the tasks, where the key is the deadline (this would allow us to find the correct position for the new task  in
in  time, as the tree height of a balanced binary search tree with
time, as the tree height of a balanced binary search tree with  leaves is
leaves is  ). We can augment
). We can augment  in the following way: store in each node not only
in the following way: store in each node not only  and
and  , but also the summation of the durations
, but also the summation of the durations  of all its descendents. This is the time that is needed to process all tasks in the subtree rooted at this node. So each node
of all its descendents. This is the time that is needed to process all tasks in the subtree rooted at this node. So each node  in
in  has three values,
has three values,  ,
,  and
and  . When we insert a new task
. When we insert a new task  into
into  , we can update this field of all ancestors of
, we can update this field of all ancestors of  and compute the finish time of
and compute the finish time of  by the time we reach the bottom of
by the time we reach the bottom of  simultaneously: initialize
simultaneously: initialize 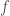 with 0. We will accumulate the time needed to process all tasks before
with 0. We will accumulate the time needed to process all tasks before  in
in 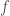 . Start from the root of
. Start from the root of  , for each node
, for each node  we touched, add
we touched, add  to
to  . If the deadline of the new task,
. If the deadline of the new task,  is greater than or equal to
is greater than or equal to  , descend to the right, and add the
, descend to the right, and add the  of the left child of
of the left child of  and
and  to
to 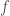 , as the tasks in the left subtree of
, as the tasks in the left subtree of  , and
, and  itself, are processed before
itself, are processed before  in the schedule; otherwise,
in the schedule; otherwise,  is less than
is less than  , in this case we descend to the left child, and do not add any value to
, in this case we descend to the left child, and do not add any value to 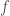 . When we reached the bottom of
. When we reached the bottom of  , we insert a new node
, we insert a new node  , for
, for  ,
,  ,
,  , and
, and  (as
(as  has no descendent other than itself).
has no descendent other than itself). 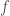 is now the partial sum
is now the partial sum  , where the summation is over all the predecessors of
, where the summation is over all the predecessors of  , in other words, all the tasks processed before
, in other words, all the tasks processed before  in the current schedule. With the finish time
in the current schedule. With the finish time 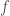 for
for  , we can compute the lateness of
, we can compute the lateness of  in the current schedule as
in the current schedule as  . The time complexity is linear in the height of
. The time complexity is linear in the height of  , as we only spend
, as we only spend  time per node as we walk down the tree. Since
time per node as we walk down the tree. Since  is balanced, the time complexity is thus
is balanced, the time complexity is thus  .
.
Let us now consider the second subproblem. How can we compute the maximum lateness of current schedule? Suppose the maximum lateness occurs after  , then we can easily get the new maximum lateness: consider any task in
, then we can easily get the new maximum lateness: consider any task in  . If this task is before
. If this task is before  in the new schedule, then the insertion of
in the new schedule, then the insertion of  has no effect on its lateness. The insertion of
has no effect on its lateness. The insertion of  causes a shift for all the tasks in
causes a shift for all the tasks in  preceded by
preceded by  by
by  time units. Therefore, their maximum lateness,
time units. Therefore, their maximum lateness,  , is now increased by
, is now increased by  . Hence, the new maximum lateness is
. Hence, the new maximum lateness is  . What about the case where the maximum lateness occurs before
. What about the case where the maximum lateness occurs before  ? Because the lateness of all the tasks preceded by
? Because the lateness of all the tasks preceded by  has increased, it is possible that one of them assumes the maximum lateness. In the worst case, if
has increased, it is possible that one of them assumes the maximum lateness. In the worst case, if  is inserted to the very front of the schedule, there would be
is inserted to the very front of the schedule, there would be 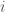 tasks after
tasks after  , even if we do not have to recompute the lateness of each of them, it is quite inefficient to get the maximum lateness by scanning each of them.
, even if we do not have to recompute the lateness of each of them, it is quite inefficient to get the maximum lateness by scanning each of them.
There are two optimizations we could make here. The first one is an observation of the lateness, the other is the use of Fenwick Tree. Let us first consider the following question: in a schedule of 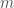 tasks,
tasks,  , ordered by their deadlines, which of these tasks might assume the maximum lateness after an insertion of a new task? Suppose we have a sequence of lateness
, ordered by their deadlines, which of these tasks might assume the maximum lateness after an insertion of a new task? Suppose we have a sequence of lateness  , where
, where  is the lateness of task
is the lateness of task 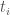 in the schedule. We make the following claim:
in the schedule. We make the following claim:
Claim: Consider a pair of tasks 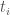 and
and  , where
, where 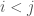 (that is, task
(that is, task 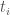 is precedes task
is precedes task  in the schedule). If
in the schedule). If  , then task
, then task 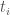 can never have a larger lateness that task
can never have a larger lateness that task  .
.
Proof: The reason is that (1) if the new task is inserted after  , both
, both 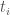 and
and  are not affected; their lateness is the same after the insertion; (2) if the new task is inserted after
are not affected; their lateness is the same after the insertion; (2) if the new task is inserted after 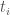 and before
and before  , the lateness of
, the lateness of 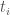 ,
,  remains the same, while
remains the same, while  increased; (3) if the new task is inserted before
increased; (3) if the new task is inserted before 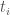 , then both
, then both 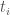 and
and  is shifted further to the right, by an amount of
is shifted further to the right, by an amount of 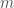 — the duration of the new task, hence if
— the duration of the new task, hence if  is no smaller than
is no smaller than  , it will remain so after the insertion.
, it will remain so after the insertion.
This observation allows us to store a sub-sequence of the lateness sequence  , which is
, which is  , where
, where  and
and  is a sub-sequence of
is a sub-sequence of  . Let us denote this list of lateness as
. Let us denote this list of lateness as  . Now we can compute the maximum lateness after the insertion of the new task: find the position where the lateness of
. Now we can compute the maximum lateness after the insertion of the new task: find the position where the lateness of  would occur in
would occur in  . Suppose
. Suppose  and
and  are the two indices. The maximum lateness is the maximum of the lateness before
are the two indices. The maximum lateness is the maximum of the lateness before  (as all tasks before and including
(as all tasks before and including  precedes task
precedes task  , so their lateness remain the same after the insertion), the lateness of
, so their lateness remain the same after the insertion), the lateness of  , and the maximum lateness of all the tasks after and including
, and the maximum lateness of all the tasks after and including  plus
plus  , which is the duration of the new task. Since the elements in
, which is the duration of the new task. Since the elements in  is in strictly decreasing order, we can easily the get the maximums of the two parts in
is in strictly decreasing order, we can easily the get the maximums of the two parts in  : the very first element of each part. Therefore, determining the maximum lateness is
: the very first element of each part. Therefore, determining the maximum lateness is  . However, we need to update the list
. However, we need to update the list  : namely, we need to add a value of
: namely, we need to add a value of  to each entry after and including
to each entry after and including  , and possibly inserting
, and possibly inserting  (the lateness of the new task) before
(the lateness of the new task) before  , and remove all the elements in the left part of
, and remove all the elements in the left part of  in order to maintain the strictly increasing order in
in order to maintain the strictly increasing order in  . (By the way, even if we don’t optimize further, and just naively update
. (By the way, even if we don’t optimize further, and just naively update  , the program already can pass all the tests on Hackerrank).
, the program already can pass all the tests on Hackerrank).
In the worst case, the size of  still could be in the order of the number of all the tasks. So the overall time complexity to update
still could be in the order of the number of all the tasks. So the overall time complexity to update  could be large (for example, if
could be large (for example, if  is inserted before all the tasks in
is inserted before all the tasks in  and each task in the optimum schedule of
and each task in the optimum schedule of  happens to have a decreasing lateness). While practically fast enough, the time complexity is still not
happens to have a decreasing lateness). While practically fast enough, the time complexity is still not  yet. To avoid many updates in
yet. To avoid many updates in  after an insertion, we use a simple trick: instead of explicitly storing the lateness in the list, we store the deadline. That is, if
after an insertion, we use a simple trick: instead of explicitly storing the lateness in the list, we store the deadline. That is, if  appears in
appears in  , in the same position, we would store
, in the same position, we would store  , which is the deadline of task
, which is the deadline of task 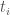 . The deadline would serve as an id for each task. Using the deadline, we can find the finish time for the task with deadline
. The deadline would serve as an id for each task. Using the deadline, we can find the finish time for the task with deadline  and hence compute its lateness in the current schedule in time
and hence compute its lateness in the current schedule in time  .
.
Now in an insertion, there might be several queries on the balanced binary search tree  for the finish times, namely, in the set of tasks precedes
for the finish times, namely, in the set of tasks precedes 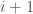 in the schedule, which also appears in
in the schedule, which also appears in  , we have to find those tasks whose lateness are smaller than the current maximum lateness and throw them out from
, we have to find those tasks whose lateness are smaller than the current maximum lateness and throw them out from  . This can be done by scanning the elements in
. This can be done by scanning the elements in  reversely from the point where
reversely from the point where 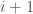 is inserted, till we find a task that precedes
is inserted, till we find a task that precedes 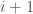 with a larger lateness, or the list is exhausted. Since each task can only be thrown away once (if it is evicted from
with a larger lateness, or the list is exhausted. Since each task can only be thrown away once (if it is evicted from  , it would never appear in
, it would never appear in  ), therefore, the overall costs of all insertions is
), therefore, the overall costs of all insertions is  .
.
After Thoughts/Alternatives
Instead of using balanced binary search tree, we could also use Fenwick Tree. Fenwick tree allows one to update an array and query partial sums on the array efficiently: each operation takes  time. In some sense, it is equivalent to balanced binary search tree. But it is much easier to implement . Although conceptually not too hard, it still takes much more lines to code an augmented balanced binary search tree than Fenwick Tree. There is a balanced binary search tree in STL, but currently I don’t know any good to augment it easily. In contrast, Fenwick tree can be easily coded using array or hash table (unordered_set in STL). Of course, we could also use a regular augmented binary search tree, without the rotation operations to keep the tree balanced, and rely on the fact that if the keys of the input for constructing the binary search tree is random, then the tree height has expectation
time. In some sense, it is equivalent to balanced binary search tree. But it is much easier to implement . Although conceptually not too hard, it still takes much more lines to code an augmented balanced binary search tree than Fenwick Tree. There is a balanced binary search tree in STL, but currently I don’t know any good to augment it easily. In contrast, Fenwick tree can be easily coded using array or hash table (unordered_set in STL). Of course, we could also use a regular augmented binary search tree, without the rotation operations to keep the tree balanced, and rely on the fact that if the keys of the input for constructing the binary search tree is random, then the tree height has expectation  .
.
be a set of
points in the plane. A block
of points in
is a set of points consecutive in
-axis. A partition of
into block is specified by a sequence of blocks
, where the blocks are pairwise disjoint, and
. Let
be the fit of the block
. The goal is to find an optimum partition
, maximizing
(the value
is not given, it is also determined by the algorithm).
by their
-coordinates. The recursion formula is straightforward: let
denotes the optimum partition of the points in
(the leftmost
points in
), for
and let
. Then
. There are totally
entries to compute, and we spend
time for the
entry, so the overall time complexity is
. Note that we assume that the function
can be obtained in
time for a block, which usually is true (by possibly preprocessing).
of
points in the plane, we would like to partition
into
blocks, and fit each block with a line. The overall cost the partition is the summation of the costs from each block.
of size
to a line
is
, where
. The “best” coefficients
and
, that is, minimizing
, has closed forms:
,
.
of the point set into segment/block, where each segment consists of a subset of
contiguous in
-axis, , let
be the optimum line fitting
, the cost of the partition is
,
is a positive real number, which encodes the penalty for partitioning
into
parts (without this term, we could fit each single point with a line, causing a trivial and meaningless optimum solution of cost 0). The goal is to find an optimum partition
minimizing
.
according their
-coordinate (in ascending order). The recursion formula is the following: define
, and define
to be an optimum partition of the first
points of
. The recursion formula is almost identical to the Bayesian Block partition problem:
, for
, where
is the optimal cost to fit the points in
with a single line (we are slightly abusing the notation here).
, following the same reasoning. One thing to note is that we need to do some preprocessing on
, so that we can quickly compute
in
time.
