Given a sequence of distinct numbers  , the sequence is a zig-zag sequence if either (1)
, the sequence is a zig-zag sequence if either (1)  , that is, an empty sequence or a sequence with a single element are both the trivial zig-zag sequence; or (2) otherwise, the sign of the difference between adjacent element alternates.
, that is, an empty sequence or a sequence with a single element are both the trivial zig-zag sequence; or (2) otherwise, the sign of the difference between adjacent element alternates.
For example, the sequence 2,3,1 is a zig-zag sequence because 2 < 3 and 3 > 1 while 1,2,3 is not. The questions are
(1) given a sequence of numbers, compute a zigzag sequence of these numbers;
(2) given  , count the number of zigzag sequences of
, count the number of zigzag sequences of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=fff&fg=444444&s=0&c=20201002) (
(![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=fff&fg=444444&s=0&c=20201002) denotes the set of elements
denotes the set of elements  ).
).
The first question is easy and it has a linear time algorithm: if the input has only 1 element, we are done. So suppose the input has at least two elements. Scan the sequence from left to right, for two adjacent element  and
and  ,
,  , if they satisfy the inequality (which is “>” for
, if they satisfy the inequality (which is “>” for 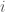 even and “<” for
even and “<” for  odd), then increment
odd), then increment 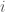 ; otherwise, swap
; otherwise, swap  and
and  . Then increment
. Then increment 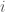 . We repeat this until we reach
. We repeat this until we reach  ..
..
As an example, consider the input 4, 1, 2, 3, 5: the target is to get a sequence  . Let’s number the elements, so
. Let’s number the elements, so  ,
,  , and so on.
, and so on.
The starting sequence is  .
.
 :
:
Since 4 > 1, we swap 4 and 1, the new sequence is 1, 4, 2, 3, 5;
 :
:
Since 4 > 2, it satisfies that  .
.
 :
:
Since 2 < 3, it satisfies that  .
.
 :
:
Since 3 < 5, we swap 5 and 3, to get 1, 4, 2, 5, 3.
The output is hence 1, 4, 2, 5, 3.
The recursive algorithm does not differ too much from the above imperative one.
A sequence ![A[1..n]](https://s0.wp.com/latex.php?latex=A%5B1..n%5D&bg=fff&fg=444444&s=0&c=20201002) is a “happy zigzag” sequence if either (1)
is a “happy zigzag” sequence if either (1)  , in which case it is a trivial happy zigzag sequence; or (2)
, in which case it is a trivial happy zigzag sequence; or (2)  ,
, ![A[1] < A[2]](https://s0.wp.com/latex.php?latex=A%5B1%5D+%3C+A%5B2%5D&bg=fff&fg=444444&s=0&c=20201002) , and
, and ![A[2..n]](https://s0.wp.com/latex.php?latex=A%5B2..n%5D&bg=fff&fg=444444&s=0&c=20201002) is a sag zigzag sequence.
is a sag zigzag sequence.
A sequence ![A[1..n]](https://s0.wp.com/latex.php?latex=A%5B1..n%5D&bg=fff&fg=444444&s=0&c=20201002) is a “sad zigzag” sequence if either (1)
is a “sad zigzag” sequence if either (1)  , in which case it is a trivial sad zigzag sequence; or (2)
, in which case it is a trivial sad zigzag sequence; or (2)  ,
, ![A[1] > A[2]](https://s0.wp.com/latex.php?latex=A%5B1%5D+%3E+A%5B2%5D&bg=fff&fg=444444&s=0&c=20201002) , and
, and ![A[2..n]](https://s0.wp.com/latex.php?latex=A%5B2..n%5D&bg=fff&fg=444444&s=0&c=20201002) is a happy zigzag sequence.
is a happy zigzag sequence.
To compute a happy zigzag sequence, if the first two elements of ![A[1..n]](https://s0.wp.com/latex.php?latex=A%5B1..n%5D&bg=fff&fg=444444&s=0&c=20201002) satisfies
satisfies ![A[1]<A[2]](https://s0.wp.com/latex.php?latex=A%5B1%5D%3CA%5B2%5D&bg=fff&fg=444444&s=0&c=20201002) , then we compute a sad zigzag sequence of
, then we compute a sad zigzag sequence of ![A[2..n]](https://s0.wp.com/latex.php?latex=A%5B2..n%5D&bg=fff&fg=444444&s=0&c=20201002) , and the output is
, and the output is ![A[1]](https://s0.wp.com/latex.php?latex=A%5B1%5D&bg=fff&fg=444444&s=0&c=20201002) concatenated with this sequence; otherwise, we swap
concatenated with this sequence; otherwise, we swap ![A[1]](https://s0.wp.com/latex.php?latex=A%5B1%5D&bg=fff&fg=444444&s=0&c=20201002) and
and ![A[2]](https://s0.wp.com/latex.php?latex=A%5B2%5D&bg=fff&fg=444444&s=0&c=20201002) , then proceed as the previous case.
, then proceed as the previous case.
getSnake :: (Ord a) => [a] -> (a->a->Bool, a->a->Bool) -> [a]
getSnake [] _ = []
getSnake [x] _ = [x]
getSnake (x:y:xs) (f,g)
|f x y = x : (getSnake (y:xs) (g,f))
|otherwise = y : (getSnake (x:xs) (g,f))
getSnake' :: (Ord a) => [a] -> [a]
getSnake' x = getSnake x ((<), (>))
The second problem is much harder than the first one. The number of zig-zag sequences for  to 7 are 1,2,5,16,61,272,1385. Look familiar? Here is the surprising connection from [1]:
to 7 are 1,2,5,16,61,272,1385. Look familiar? Here is the surprising connection from [1]:

 .
.
An interesting object is the following zigzag triangle from [1]:
1
0 1
1 1 0
0 1 2 2
5 5 4 2 0
0 5 10 14 16 16
61 61 56 46 32 16 0
The triangle is filled in the following way: the first row is 1. The  row is computed from the
row is computed from the  row: we alternate the direction of filling up the row, and the starting element is 0. We fill up the row using the zig-zag rule:
row: we alternate the direction of filling up the row, and the starting element is 0. We fill up the row using the zig-zag rule:
a
b -> (a+b)
The key observation is that the  element in
element in  row is the number of zigzag sequence ending with
row is the number of zigzag sequence ending with 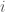 : for example, for
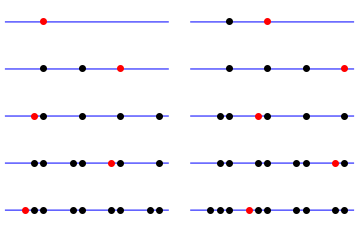
: for example, for  , the zigzag sequences are the following (sorted by ending element):
, the zigzag sequences are the following (sorted by ending element):
[[3,4,2,5,1],[2,5,3,4,1],[3,5,2,4,1],[2,4,3,5,1],[4,5,2,3,1],[1,4,3,5,2],[4,5,1,3,2],[1,5,3,4,2],[3,5,1,4,2],[3,4,1,5,2],[1,4,2,5,3],[1,5,2,4,3],[2,5,1,4,3],[2,4,1,5,3],[2,3,1,5,4],[1,3,2,5,4]]
The fifth row in the zigzag triangle is 5, 5, 4, 2, 0. This connection also gives an efficient recursive algorithm to count the number of zigzag sequences.
Update:
(1) The zigzag sequence is essentially alternating permutation.
(2) The recursive algorithm (getSnake) above can also be used to find a longest alternating permutation in quadratic time.
Reference
[1] Some Very Interesting Sequences, John H. Conway and Tim Hsu. (link)